Revised Version 2
Thanks to Jorge Carballeira who found the error
Full screen
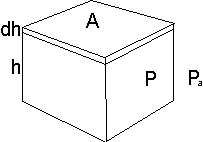 Consider a box. It is is h high and has a top and bottom area of A units.
Consider a box. It is is h high and has a top and bottom area of A units.
Let's be simplistic and use Charles's law that states p*v is constant for a
given volume of gas provided the temperature stays constant.
So for a given starting pressure P0 and volume V0 we can
deduce any later pressure as p = P0*V0 / v
But since the volume is v=h*A we can reason that
p = P0*V0/(h*A)
Now if we let the gas expand just a teeny bit (a distance dh) the work done (dW)
is the distance moved multiplied by the force applied
Force is (p - Pa) * A so
dW = ((P0*V0)/(h*A) - Pa) * A * dh
dW = (P0*V0/h - Pa*A) * dh
So now we want to sum all the dW for all the dh for a range of h from our initial
pressure/volume until the pressure reaches Pa.
So the initial limit is based on v=h*A giving h = V0/A
and the closing limit is based on p = P0 * V0 / (h * A)
so for p=Pa we get h = P0*V0/(Pa * A)
W = integrate((P0*V0/h - Pa*A) * dh) using limits above
W = P0*V0 * integrate(h-1*dh) - A * Pa * integrate(dh)
W = P0*V0 * [logeh] - A * Pa * [h]
substitute in the initial and final values for h
W = P0*V0 * (loge(P0*V0/(A * Pa)) - loge(V0/A)) - A * Pa * (P0*V0/(A * Pa) - V0/A)
since log(a)-log(b) = log(a/b) we can simplify this a bit
W = P0*V0 * (loge((P0*V0/(A*Pa))/(V0/A)) - A*Pa*(P0*V0/(A*Pa)-V0/A)
now it all comes together with basic algebra
W = P0*V0 * loge(P0/Pa) - P0*V0 + Pa*V0
W = P0*V0 * (loge(P0/Pa)-1) + Pa*V0
Well I could use this but it's messy and I only want a feel for the numbers.
P0/Pa is the tank pressure divided by normal air pressure and
loge of 200 is 5.3 and loge of 300 is 5.7 so I'll call
it 5.5 also Pa*V0 is pretty trivial beside the first term
so it all becomes:
W = P0*V0* 4.5
Great. Just need to sort out the units.
The world in general seems to have settled for MKS (Meters/Kilograms/Seconds)
as a way to do business in physics but I'd prefer litres and bar here.
1 bar is 105 Newtons/square meter and 1 litre is 10-3
cubic meters so our formula becomes
W (in Joules) = P0*V0*450
You're not impressed? You don't have a feel for a joule perhaps?
A joule is one watt for one second. so 1242000 joules is 3 kilowatts
for just under 7 minutes.
That would boil 3.5 litres of water and so make coffee for everybody on the boat?
Still doesn't seem much does it? The trick is to release it in an instant.
In a previous life (see CV) I used a unit of energy that was 4.184x1012
joules representing the energy released by 1000 tons of TNT.
That works out at about 1866000 joules per pound.
In metric units the tank contains the energy in 300 grams of TNT.
A normal hand grenade has about 150 grams.
Hum. That works out at 650 grams for my 10L twins at 300 bar.
Just behind my head? Now I see why people worry about it.
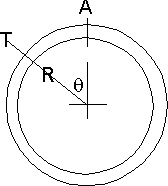 Consider a bit of tank wall. The radius is R and the thickness is T. We will
work on a slice of this W long rather than do the whole tank.
Consider a bit of tank wall. The radius is R and the thickness is T. We will
work on a slice of this W long rather than do the whole tank.The force on A can therefore be the sum of all the right hand components of the pressure on the wall for all values of θ from 0 to π/2
Well for a vanishingly small slice of θ ie. dθ we have an area W*R*dθ
so if the pressure difference across the wall is P a force of W*R*P*dθ
The horizontal component is then W*R*P*sinθ*dθ
so integrating from 0 to π/2
we get W*R*P*(-cos(π/2)+cos(0))) = 2*W*R*P
We want to use the Young's modulus values for the tank material and this is the ratio of the stress to the strain. ie: m = (force/unit area)/fractional increase in length
Now the piece of than wall this acts on is a the a area at A which is W*T so
the stress is 2*W*R*P/W*T giving 2*R*P/T
so the stretch is 2*R*P/(T*m)
Now the energy in a even stretch is ½ * force * distance
The distance stretched is the circumference * the strain ie:
D = 4*R2*π*P/(T*m)
giving an energy of
E = 4*R3*π*P2*W/(T*m)
OK so lets try some numbers in MKS units again using one of my 10L tanks.
R = 0.09 meters
P = 300x105N/sq meter (300 bar)
W = 0.45 meters
m = 2x1011 for steel
T is a problem but to a first order guess the tanks weigh 16Kg so that is virtually 2 Litres = 0.002 cu meters to make a cylinder 0.5m long by 0.5m circumference leaving 0.008m (0.8cms for the wall)
Bang all the numbers in and we get 2319 joules
less than 0.2% of the air. So that's all right then I suppose.